haogui

空间节省：位图，布隆过滤器， Roaring Bitmap

​ 三种数据结构共同点为都是以0,1为基础，适用于判断某个东西是否存在

位图

​ 位图即是一种数组的数据结构，但其元素里面的内容只能是0,1。用于判断一个有限区间元素是否存在。如下图所示

a[6]=1,表示6号元素存在。那什么是6号元素？可以是一个字符的ASC码，可以是一个字符串的hash值对数组大小的取模。此种数据结构的思想为数组下面代表多少号元素，数组元素的值代表其是否存在，能够极大节省空间。可能你又会有疑问？如果我使用的语言没有提供0,1的这种占1个位的数据类型，我应该怎么做呢？

我们往往需要对其他类型的数组进行一些转换设计，使其能对相应的 bit 位的位置进行访问，从而实现位图。我们以 char 类型的数组为例子。

​ 假设我们申请了一个 1000 个元素的 char 类型数组，每个 char 元素有 8 个 bit，如果一个 bit 表示一个用户，那么 1000 个元素的 char 类型数组就能表示 8*1000 = 8000 个用户。如果一个用户的 ID 是 11，那么位图中的第 11 个 bit 就表示这个用户是否存在的信息。这种情况下，我们怎么才能快速访问到第 11 个 bit 呢？

首先，数组是以 char 类型的元素为一个单位的，因此，我们的第一步，就是要找到第 11 个 bit 在数组的第几个元素里。具体的计算过程：一个元素占 8 个 bit，我们用 11 除以 8，得到的结果是 1，余数是 3。这就代表着，第 11 个 bit 存在于第 2 个元素里，并且在第 2 个元素里的位置是第 3 个。

​ 对于第 2 个元素的访问，我们直接使用数组下标[1]就可以在 O(1) 的时间内访问到。对于第 2 个元素中的第 3 个 bit 的访问，我们可以通过位运算，先构造一个二进制为 00100000 的字节（字节的第 3 位为 1），然后和第 2 个元素做 and 运算，就能得知该元素的第 3 位是 1 还是 0。这也是一个时间代价为 O(1) 的操作。这样一来，通过两次 O(1) 时间代价的查找，我们就可以知道第 11 个 bit 的值是 0 还是 1 了。

​ 一道可以用上面数据结构思想的简单算法题：一个英文的字符串让你判断每个字符出现的次数(要求空间尽可能使用的少)？

布隆过滤器

​ 当你写一个爬虫爬取博客时，要求不进行重复爬取。你会怎么设计？使用一个容器存储所有爬取过的完整网址吗？当你爬取了上亿的url时，如果你存了这些完整的url，空间消耗巨大。因此我们要怎样才能节省空间呢。你可能会想使用一个hash函数计算出hash值，再用bitmap存储。很好空间节省了，但hash冲突会不会很大？于是bloomfilter出现了。

​ 布隆过滤器最大的特点，就是对一个对象使用多个哈希函数。如果我们使用了 k 个哈希函数，就会得到 k 个哈希值，也就是 k 个下标，我们会把数组中对应下标位置的值都置为 1。布隆过滤器和位图最大的区别就在于，我们不再使用一位来表示一个对象，而是使用 k 位来表示一个对象。这样两个对象的 k 位都相同的概率就会大大降低，从而能够解决哈希冲突的问题了。

​ bloomfilter,使用多个hash函数分别将这一个url的hash算出来，随后在bitmap中进行标记。如下图所示使用三个hash函数进行计算后标记

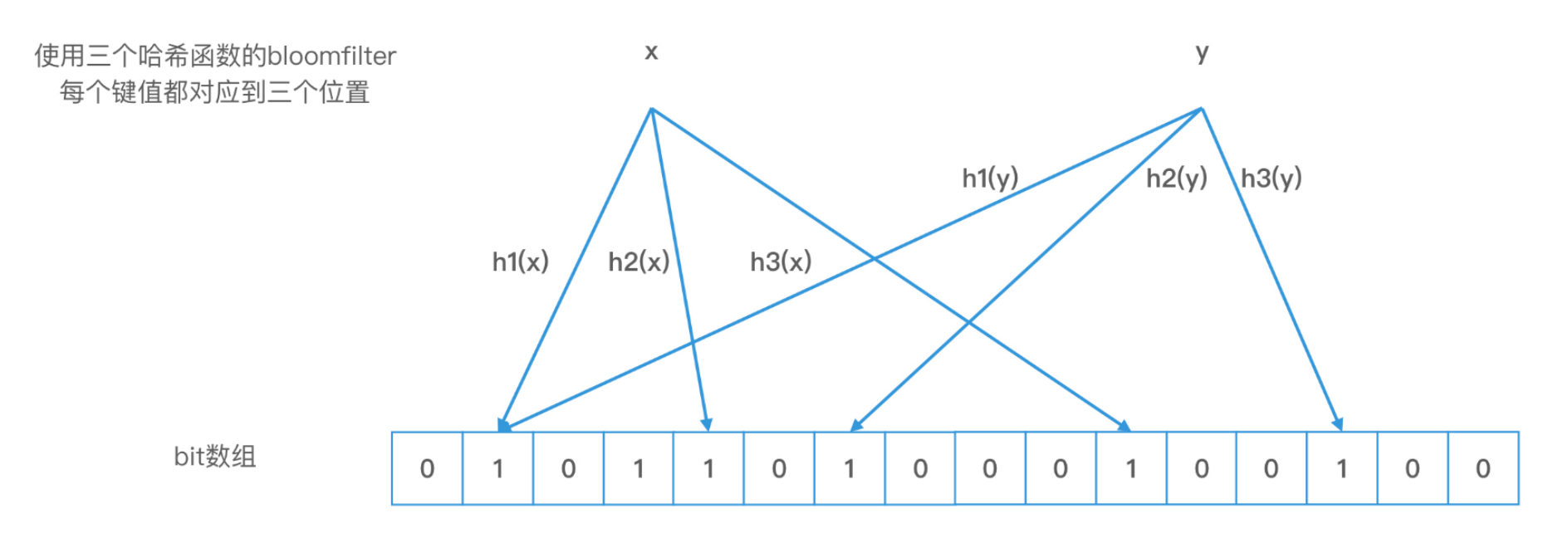
但是，布隆过滤器的查询有一个特点，就是即使任何两个元素的哈希值不冲突，而且我们查询对象的 k 个位置的值都是 1，查询结果为存在，这个结果也可能是错误的。这就叫作布隆过滤器的错误率。

​ 对于布隆过滤器而言，如果哈希函数的个数不合理，比如哈希函数特别多，布隆过滤器的错误率就会变大。因此，除了使用多个哈希函数避免哈希冲突以外，我们还要控制布隆过滤器中哈希函数的个数。有这样一个**计算最优哈希函数个数的数学公式: 哈希函数个数 k = (m/n) * ln(2)。**其中 m 为 bit 数组长度，n 为要存入的对象的个数。实际上，如果哈希函数个数为 1，且数组长度足够，布隆过滤器就可以退化成一个位图。所以，我们可以认为“位图是只有一个特殊的哈希函数，且没有被压缩长度的布隆过滤器”

Roaring Bitmap

​ 升级版位图 roaring bitmap。在使用位图的时候当元素个数很少，比较稀疏时你又会觉得空间有点浪费。比如一个元素的取值范围是int32位，则你需要2的32次方bit = 2 ** 29 byte = 2 ** 19k = 2 ** 9 M = 512M。而一开始元素个数有很少这对于空间的浪费还是不小。于是有了 roaring bitmap

​ 下面我们来学习一下 Roaring Bitmap 的设计思想。

​ 首先，Roaring Bitmap 将一个 32 位的整数分为两部分，一部分是高 16 位，另一部分是低 16 位。对于高 16 位，Roaring Bitmap 将它存储到一个有序数组中，这个有序数组中的每一个值都是一个“桶”；而对于低 16 位，Roaring Bitmap 则将它存储在一个 2^16 的位图中，将相应位置置为 1。这样，每个桶都会对应一个 2^16 的位图。

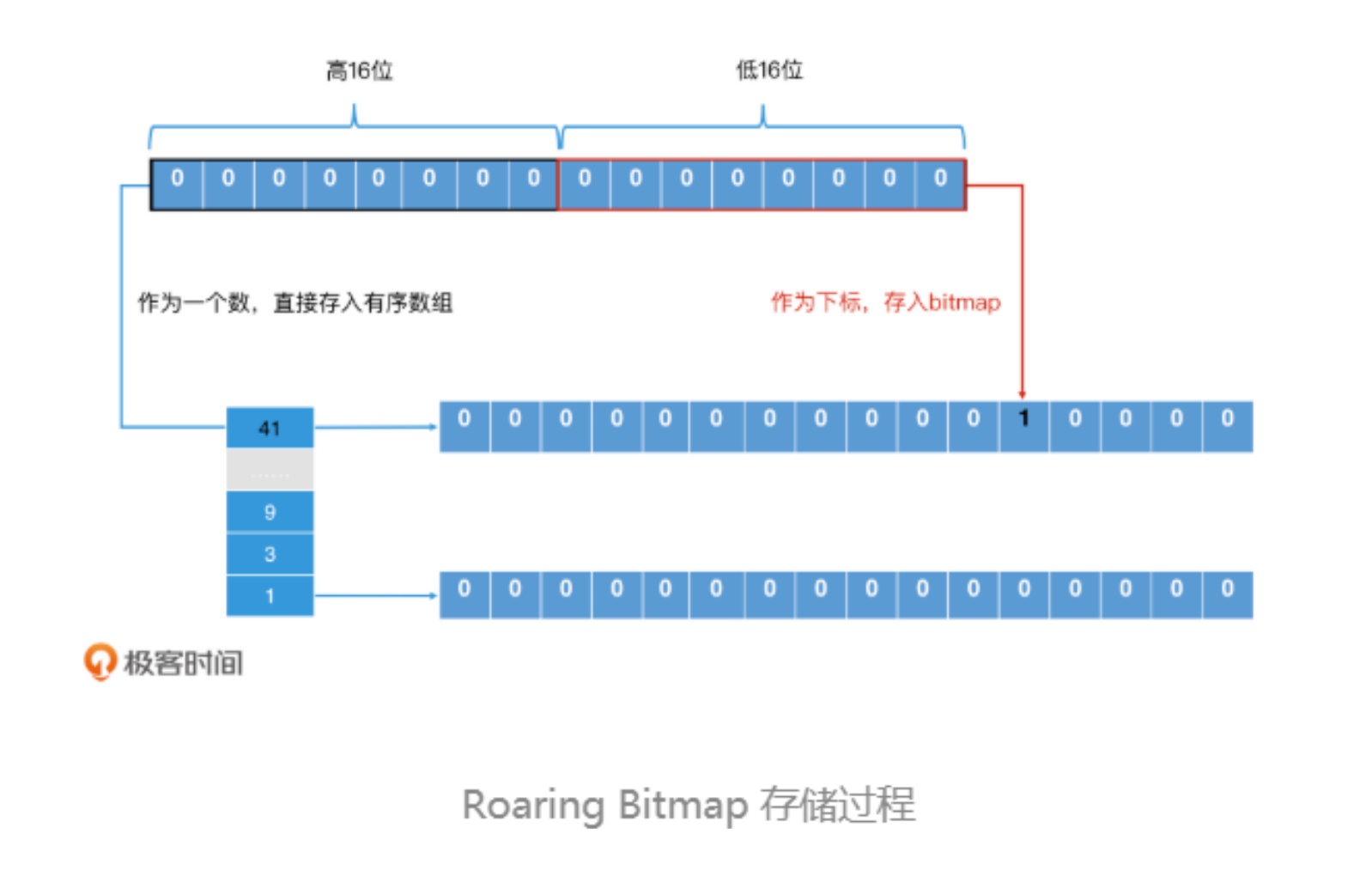
​ 再计算一下空间的节省 2 ** 16bit =2 ** 13 byte = 2**3k = 8k 。一个桶8k，当比较稀疏时占用的桶比较小。空间节省就会由上面的512M节省至 n×8k。

​ 在实际工业项目中会将bitmap与roaring bitmap结合使用，当到达某个阈值则将roaring bitmap转换为bitmap

上述三种数据结构一般用于快速判断是否某个东西存在，在空间上也很节省

空间索引

​ 前面的数据结构用于快速判断是否存在，现在我们来讲讲怎么快速查找你邻近的人。

Geohash实现附近人

​ 如何快速查找你附近的人？首先你需要编码，把每个地区都进行编码，编码格式如下图所示。

在水平方向上，我们用 0 来表示左边的区域，用 1 来表示右边的区域；在垂直方向上，我们用 0 来表示下面的区域，用 1 来表示上面的区域。因此，这四个区域，从左下角开始按照顺时针的顺序，分别是 00、01、11 和 10

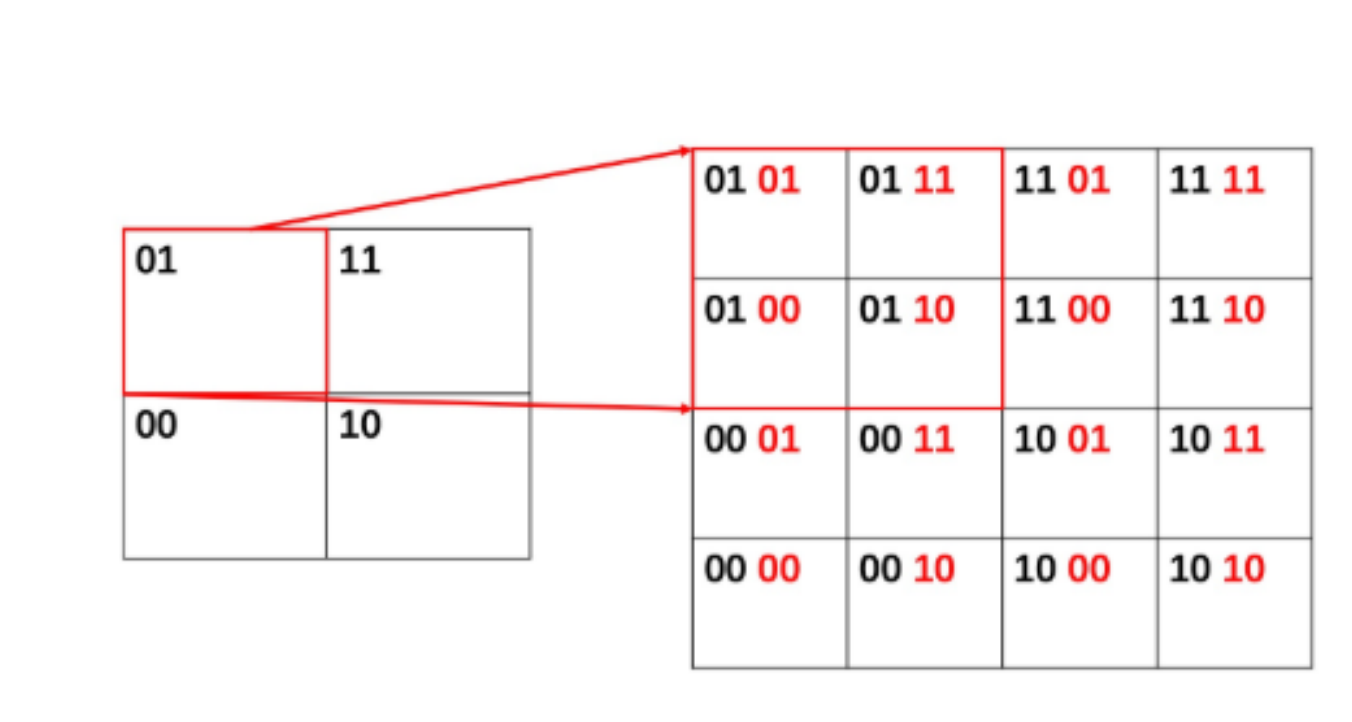
这样编码后你是不是立马就知道你附近地址的编码了，并能快速检索

这种区域编码的方式有 2 个优点：

1. 区域有层次关系：如果两个区域的前缀是相同的，说明它们属于同一个大区域；
2. 区域编码带有分割意义：奇数位的编号代表了垂直切分，偶数位的编号代表了水平切分，这会方便区域编码的计算（奇偶位是从右边以第 0 位开始数起的）。

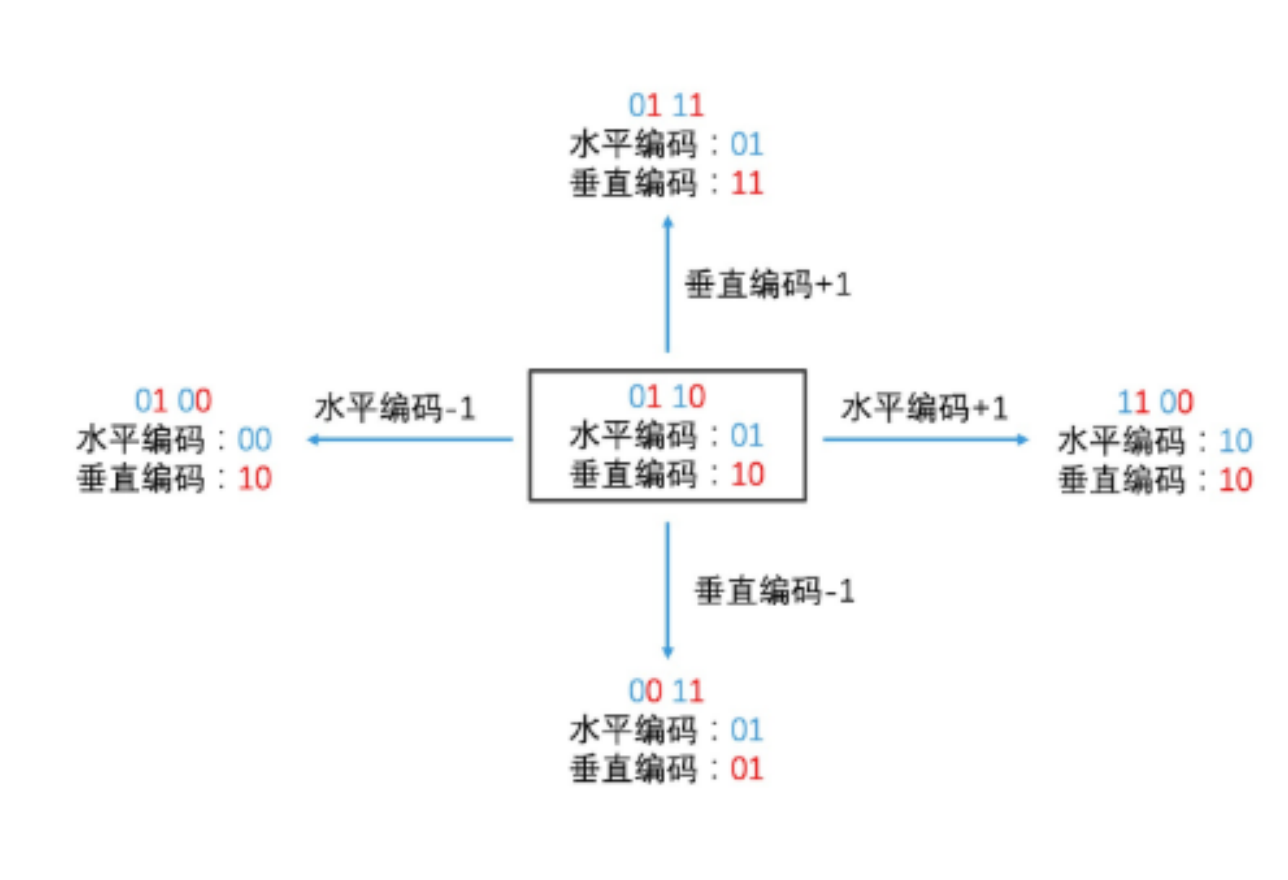
每个地方都有经度和纬度，于是我们能够按照某个人在地理上的具体位置，来对他进行编码

例如：

​ 我们知道，地球的纬度区间是[-90,90]，经度是[-180,180]。如果给出的用户纬度（垂直方向）坐标是 39.983429，经度（水平方向）坐标是 116.490273，那我们求这个用户所属的区域编码的过程，就可以总结为 3 步：

1. 在纬度方向上，第一次二分，39.983429 在[0,90]之间，[0,90]属于空间的上半边，因此我们得到编码 1。然后在[0,90]这个空间上，第二次二分，39.983429 在[0,45]之间，[0,45]属于区间的下半边，因此我们得到编码 0。两次划分之后，我们得到的编码就是 10。

2. 在经度方向上，第一次二分，116.490273 在[0,180]之间，[0,180]属于空间的右半边，因此我们得到编码 1。然后在[0,180]这个空间上，第二次二分，116.490273 在[90,180]之间，[90,180]还是属于区间的右半边，因此我们得到的编码还是 1。两次划分之后，我们得到的编码就是 11

3. 我们把纬度的编码和经度的编码交叉组合起来，先是经度，再是纬度。这样就构成了区域编码，区域编码为 1110。

这样得到的编码会特别长，那为了简化编码的表示，我们可以以 5 个比特位为一个单位，把长编码转为 base32 编码，最终得到的就是 wx4g6y。这样 30 个比特位，我们只需要用 6 个字符就可以表示了。

随后什么是Geohash ，这种将经纬度坐标转换为字符串的编码方式，就叫作 Geohash 编码。

按照位置存储信息

​ 为了方便索引以及对范围查找更加友好，按照Geohash能够快速检索，但如何按照GeoHash进行存储。给出答案四叉树结构如下所示

每一个的子节点最多4个 即 00,01,10,11。

你可能会想Geohash是字符串这样怎么存储呢？ 答案 前缀树

前缀树在敏感词过滤中常用能够压缩空间，前缀输的结构如下如所示

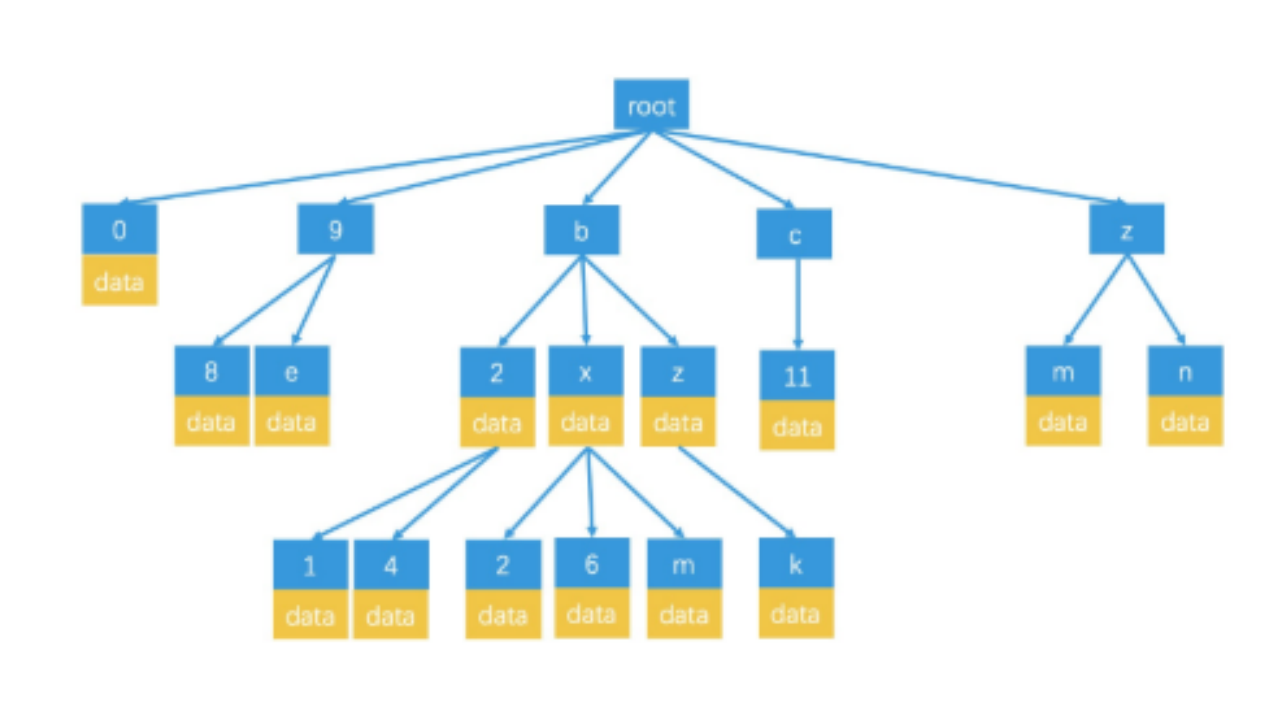
局部hash算法快速过滤

​ 介绍一下在搜索引擎中如果快速过滤相似文章。

在空间向量中进行临近索引

​ 计算2篇文章的相似性，常见方法之一就是使用空间向量模型，所谓向量空间模型，就是将所有文档中出现过的所有关键词都提取出来。如果一共有 n 个关键词，那每个关键词就是一个维度，这就组成了一个 n 维的向量空间。

那一篇文档具体该如何表示呢？我们可以假设，一篇文章中有 k（0<k<=n）个关键词，如果第 k 个关键词在这个文档中的权重是 w，那这个文档在第 k 维上的值就是 w。一般来说，我们会以一个关键词在这篇文档中的 TF-IDF 值作为 w 的值。而如果文章不包含第 k 个关键词，那它在第 k 维上的值就是 0，那我们也可以认为这个维度的权重就是 0。这样，我们就可以用一个 n 维的向量来表示一个文档了，也就是 <w1,w2,w3,……wn>。这样一来，每一个文档就都是 n 维向量空间中的一个点。

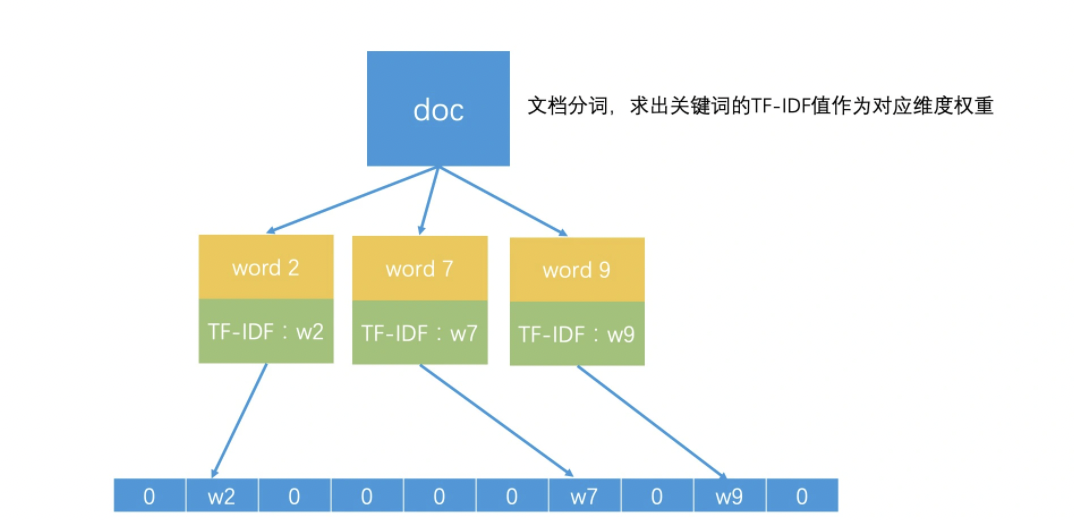
​ 如此一来，就把计算相似度量化了，每个维度距离越相近，则越相似

局部敏感哈希

​ 我们可以利用哈希的思路，将高维空间中的点映射成低维空间中的一维编码。换句话说，我们通过计算不同文章的哈希值，就能得到一维哈希编码。如果两篇文章内容 100% 相同，那它们的哈希值就是相同的，也就相当于编码相同。

​ 不过，如果我们用的是普通的哈希函数，只要文档中的关键词有一些轻微的变化（如改变了一个字），哈希值就会有很大的差异，于是工业界设计了一种hash函数，可以让相似的数据通过hash，生成的哈希值是相近的（甚至是相等的）这种哈希函数就叫作局部敏感哈希（Locality-Sensitive Hashing）。

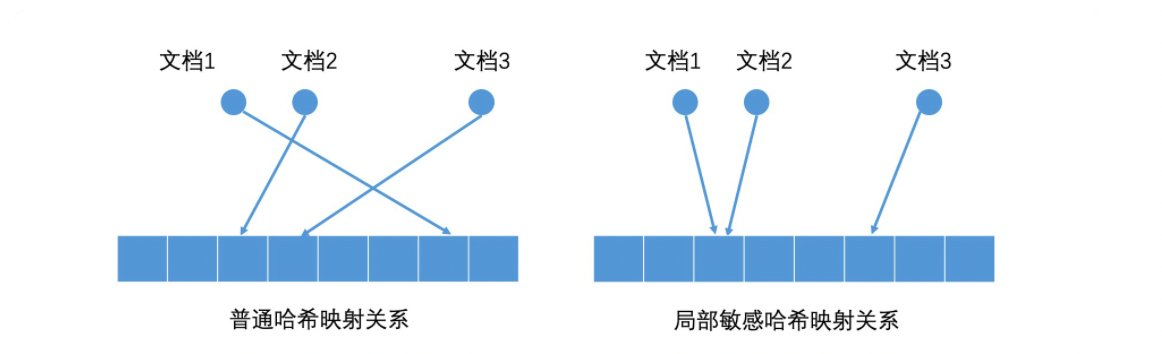
如何理解局部敏感hash实现

​ 其实局部敏感哈希并不神秘。让我们以熟悉的二维空间为例来进一步解释一下。

​ 在二维空间中，我们随意划一条直线就能将它一分为二，我们把直线上方的点的哈希值定为 1，把直线下方的点的哈希值定为 0。这样就完成一个简单的哈希映射。通过这样的随机划分，两个很接近的点被同时划入同一边的概率，就会远大于其他节点。也就是说，这两个节点的哈希值相同的概率会远大于其他节点。

​

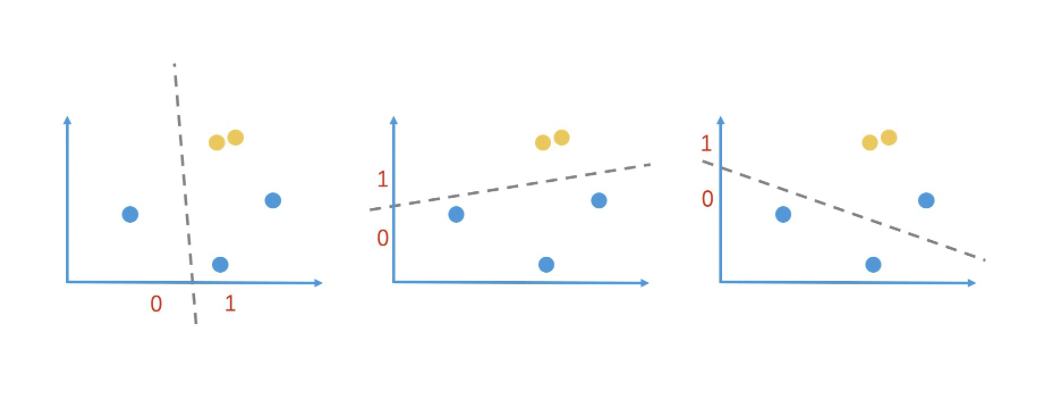
​ 当然，这样的划分有很大的随机性，不一定可靠。但是，如果我们连续做了 n 次这样的随机划分，这两个点每次都在同一边，那我们就可以认为它们在很大概率上是相近的。因此，我们只要在 n 次随机划分的过程中，记录下每一个点在每次划分后的值是 0 还是 1，就能得到一个 n 位的包含 0 和 1 的序列了。这个序列就是我们得到的哈希值，也就是区域编码。

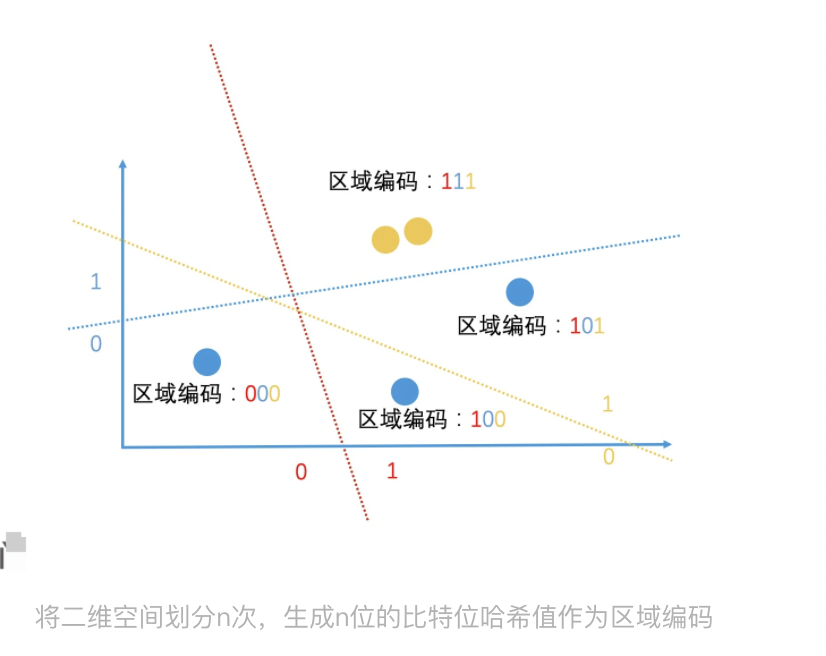
​ 随后计算其海明距离(有两个哈希值，比特位分别为 00000 和 10000。你可以看到，它们只有第一个比特位不一样，那它们的海明距离就是 1。如果我们认为海明距离在 2 之内的哈希值都是相似的，那它们就是相似的。)，

SimHash

​ 这种构造局部敏感哈希函数的方式也有一些缺陷：在原来的空间中，不同维度本来是有着不同权重的，权重代表了不同关键词的重要性，是一个很重要的信息。但是空间被 n 个超平面随机划分以后，权重信息在某种程度上就被丢弃。

​ google提出了SimHash，步骤如下

1. 选择一个能将关键词映射到 64 位正整数的普通哈希函数。
2. 使用该哈希函数给文档中的每个关键词生成一个 64 位的哈希值，并将该哈希值中的 0 修改为 -1。比如说，关键词 A 的哈希值编码为 <1,0,1,1,0>，那我们做完转换以后，编码就变成了 <1,-1,1,1,-1>。
3. 将关键词的编码乘上关键词自己的权重。如果关键词编码为 <1,-1,1,1,-1>，关键词的权重为 2，最后我们得到的关键词编码就变成了 <2,-2,2,2,-2>。
4. 将所有关键词的编码按位相加，合成一个编码。如果两个关键词的编码分别为 <2,-2,2,2,-2> 和 ❤️,3,-3,3,3>，那它们相加以后就会得到 <5,1,-1,5,1>。
5. 将最终得到的编码中大于 0 的值变为 1，小于等于 0 的变为 0。这样，编码 <5,1,-1,5, 1> 就会被转换为 <1,1,0,1,1>。

如何对相似索引进行检索

​ 如果要检索海明距离为3的为例，要如何进行检索呢？

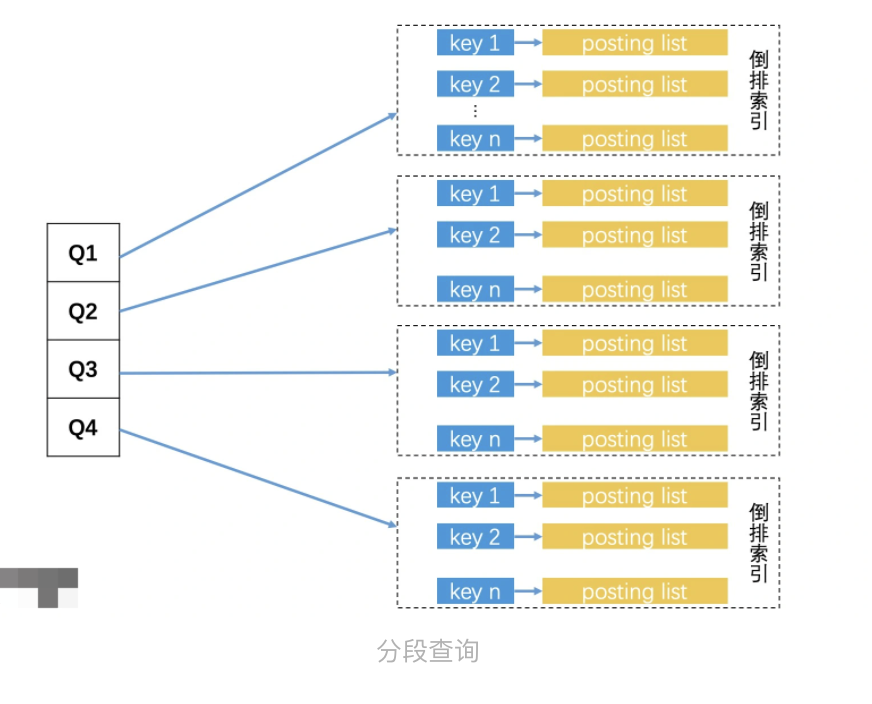
方法一：遍历，为64个比特位，每个比特位做一个索引，一共有 64 个比特位，也就一共有 2*64 共 128 个不同的 Key。因此我们可以使用倒排索引。某一个位置相同的取出，在一个一个比较。效率极低只有比特位完全不同的才回过滤。按照概率只能过滤掉二分之一的64次方的。

google使用的是抽屉原理进行优化

抽屉原理

​ 三个苹果放入四个抽屉总有一个是空的，如果要求海明距为三则可以把64个比特位分为4段，如果想要海明距小于等于三，则4段中起码有一段是要完全相同，由此可直接过滤掉四分之一的数据

具体实现

​ 根据这个思路，我们可以将每一个文档都根据比特位划分为 4 段，以每一段的 16 个比特位的值作为 Key，建立 4 个倒排索引。检索的时候，我们会把要查询文档的 SimHash 值也分为 4 段，然后分别去对应的倒排索引中，查询和自己这一段比特位完全相同的文档。最后，将返回的四个 posting list 合并，并一一判断它们的的海明距离是否在 3 之内。