红黑树定义

本文来讲一讲红黑树,但不涉及过多源码,讲究点到为止(个人觉得太抠细节没意思,当然我也没有扣),领会到奥义就行。
定义
这是绕不开的圈子,先说其定义
- 根节点是黑色
- 每个叶子结点都是黑色的空节点,也就是说叶子结点不存储数据
- 任何相邻的节点不能同时是红色,也就是说红色节点会被黑色节点分开
- 每个节点,从该节点到达其可达的叶子节点,包含相同的黑色节点(即从某个节点出发,到达叶子节点经过的黑色节点数量一致)
图示
下图是取自别人博客中的图片,去掉了黑色的、空的叶子节点
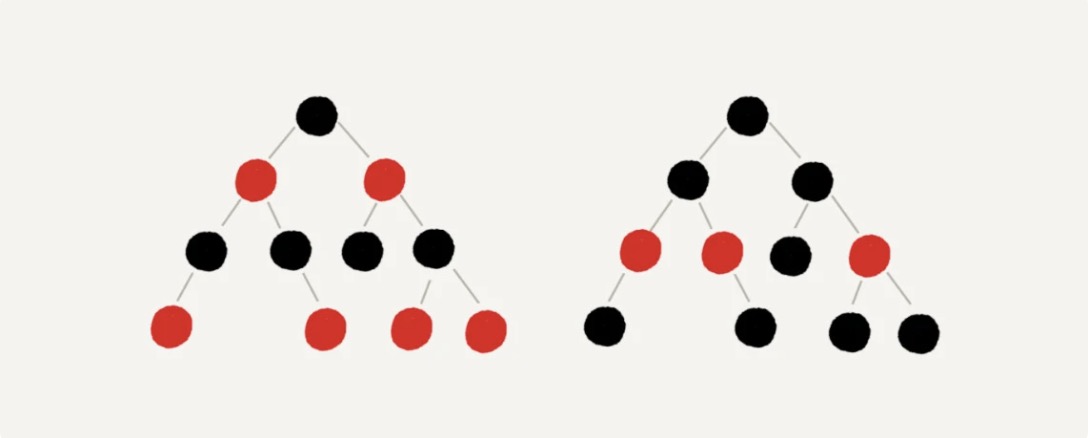
平衡二叉查找树的初衷,是为了解决二叉查找树因为动态更新导致的性能退化问题。所以,“平衡”的意思可以等价为性能不退化。“近似平衡”就等价为性能不会退化得太严重。
我们来分析红黑树的搜索效率。
我们将红色节点从上图中进行删除
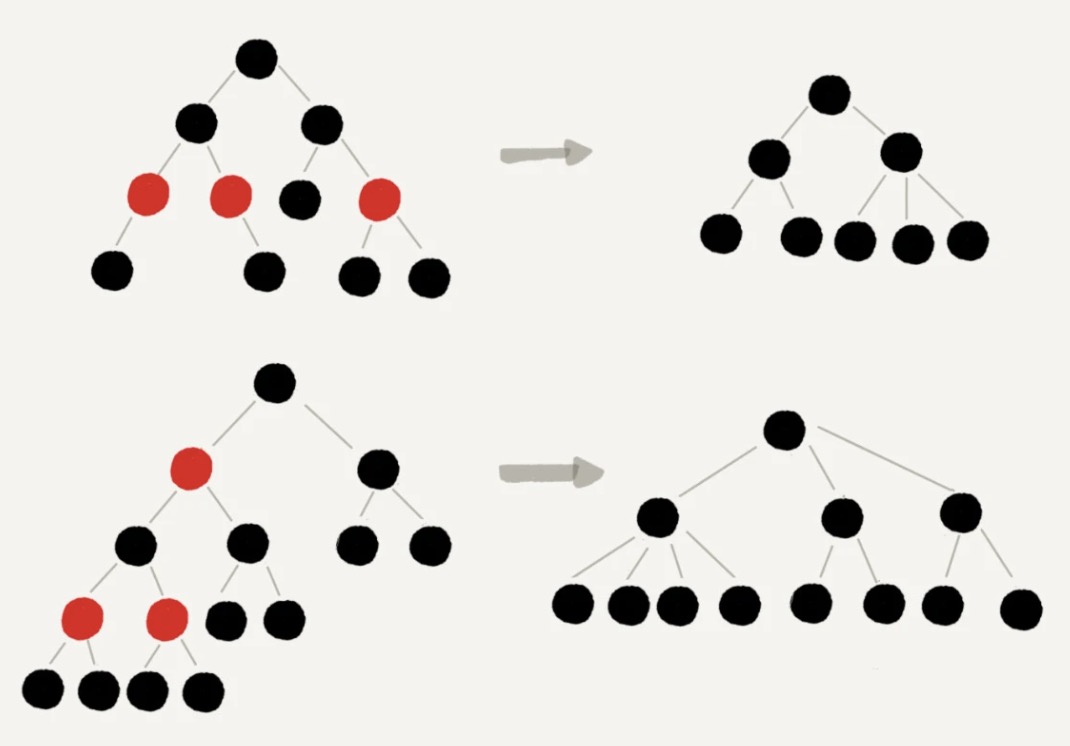
你会发现他变成了一颗2,3,4树,那他的查找效率是多大呢?log2n,log3n,log4n 反正呢不回比平衡二叉树log2n慢。
随后我们加入红色节点,从定义3可知:在红黑树中,红色节点不能相邻,也就是说,有一个红色节点就要至少有一个黑色节点,将它跟其他红色节点隔开。红黑树中包含最多黑色节点的路径不会超过 log2n,所以加入红色节点之后,最长路径不会超过 2log2n,也就是说,红黑树的高度近似 2log2n。
但其实其查找可能是2log2n,2log3n,2log4n ,所以平均下来速率应该快于平衡二叉树。
2,3,4树
如果真想弄清楚这红黑树是怎么旋转和转变的,建议观看以下文章,在此给大家重定向
http://itpcb.com/a/104477 ----2,3,4树与红黑树之间的变换
https://algs4.cs.princeton.edu/33balanced/ ---- 红黑树作者博客